Where do the values in the Z-table come from?
By: Krista Floer
In statistics, one of the most important curves is the Normal Curve. Multiple theorems and formulas were created based on the properties of this curve. Most statistics students are just given a table of values found by using this curve, but a more useful instructional strategy would be to develop the function that calculates all of the values in the given table. The table I am talking about is the z-table. AP Statistics students know the formula to find the z-score of a data point, but many of them do not know where the values on the table come from. First, we need to know that exponentiating a quadratic function yields a normal distribution. Let’s look at an image from the Graphing Calculator software:
The exponentiated graph may seem a little unexpected at first, but by considering the properties of the exponential function we can begin to see why the graph looks like it does.
A property of the exponential function is that it will always be positive. This means that it has an asymptote at y = 0, also known as the x-axis. I am only talking about the parent function, 
. Transformations can be applied so that the function can yield negative outputs. But for the purposes of this essay, we will only consider the parent function.
is similar to the curve that we want, but it is not the exact curve that we are looking for. To change the intercepts and asymptotes of the curve, we need more variable. Let’s plot the function .
We need to investigate what a, b, and c do to the equation. Before we look at 
, let’s first look at 
to investigate what a, b, and c each do the quadratic function. First, let’s look at the function as a changes and b and c are held constant:
We can see that a controls whether the parabola opens upward or downward. If a is positive, then the parabola opens upward. If a is negative, then the parabola opens downward.
Now, let’s look at the function as b changes and a and c are held constant::
We see that b controls where the vertex of the parabola is horizontally.
Now, let’s look at the function as c changes and a and b are held constant:
We see that c controls where the vertex of the parabola is vertically.
Now we can better understand how the changes of a, b, and c will affect the exponentiated quadratic function.
First, look at a:
Since in this graph, a controlled whether the parabola opened up or down, we know that a will need to be less than 0 for us to get closer to finding the equation that will give us the normal curve.
Now look at b:
We see that b controls how wide the peak or valley in the graph is.
Now look at c:
We can see that c controls the height of the hump in the curve.
The steps to finding the equation for the normal curve in this fashion will stop here. There is not a simple way of explaining where the numbers in the actual function come from in this method of finding a curve. Hence we need to start from a different direction.
We can start with the Gaussian Function: 
, where 
, b = Mu, and c = sigma.
Since we want the normal curve, we want it to be centered at 0 (Mu = 0) with a standard deviation of 1 (sigma = 1) because that is the definition of the normal curve.
So now if we substitute again, we get the following: 
, which simplified gives 
.
This is what is known as the probability density function for the normal curve. That is, this is the function that gives us the normal curve. From this curve, we can calculate the probability of any number after it has been standardized to a Z-score.
I want to ask the question, where does the empirical rule come from?
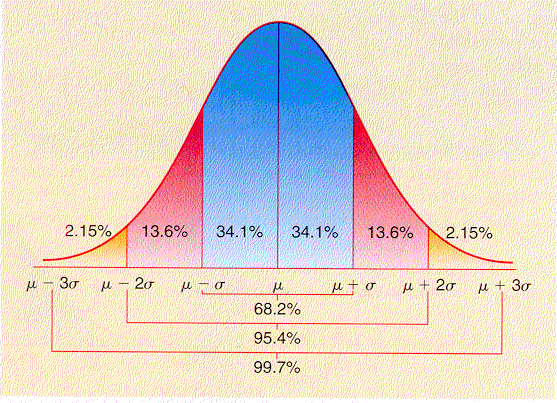
As seen in the picture above, the empirical rule is:
One standard deviation away from the mean contains 68.4% of the data.
Two standard deviations away from the mean contain 95.6% of the data.
Three standard deviations away from the mean contain 99.8% of the data.
From the Empirical Rule we know that almost all of the data in a normal distribution should be contained within three standard deviations of the mean. But how did this come about?
The z-table uses the Probability Density Function to find the probability for any given z-value. For one standard deviation, we want the area under the curve from (-1, 1). To do this, we find the z-score for 1 and then subtract the z-score for -1. z-score for 1 = .8413 z-score for -1 = .1587 So .8413 - .1587 = .6826. Hence total amount of data that is within one standard deviation of the mean is 68.26%. The same can be done for 2 standard deviations and 3 standard deviations. We probably use 1, 2, and 3 standard deviations because those numbers are whole numbers. Most people like using whole numbers as reference points, so iot seems that human nature dictated that we use whole number standard deviations from the mean.
But where did these values come from?
To answer this question, we need some calculus. Travel back to when you were learning integral calculus. One of the first things you learn is that to find the area underneath a curve, you take the intergral of the function on a given interval. We have a function, .
The probability of any given x is found by computing the area underneath the curve that our function makes. So if we want to find the area under the curve from -1 to 1 (which would be within one standard deviation of the mean for the normal curve), then we do the following:
∫ 
dx (interval -1 to 1).
After simplifying all the algebra, we get .6826, which is the same as what we saw in the empirical rule above. So we can see that the entire table of values in a z-table was found doing this integration over and over and over for different intervals to get each value. It seems logical that a table would be made because the table is just a bunch of calculus problems that were solved and compiled in an easy to read manner. Now, students or anyone can use the z-table without knowing how to do definite integrals.